判断点是否在一个凸多边形内部，可以根据面积、叉乘的方法判断。但是包括凹多边形的时候，就得使用射线法判断。下面介绍这种算法。

算法原理

奇-偶规则（Odd-even Rule）：奇数表示在多边形内，偶数表示在多边形外

从任意位置p作任意方向的一条射线，若与该射线相交的多边形边的数目为奇数，则p是多边形内部点，否则是外部点。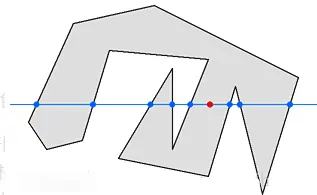
Preview
以上图为例：从红点向任意方向发射射线(上图是向左和向右)，与图形的边的交点总和为奇数时，点在内部；为偶数时，点在外部。（上图向左有5个点，向右有3个点），所以红点在多边形的内部。所以，问题就从判断点在多边形的内部转化为了：判断点朝任意方向的射线与多边形的边的交点个数的奇、偶问题。

如何判断射线与多边形的交点？

Preview
从上图可以非常直观地看出，取出多边形中两个相邻的点P1、P2，根据两点得到直线的方程为：Y=(y1-y2)/(X1-X2)*（X - X1）+Y1。
将待监测点P0的X0代入直线方程（如果向上打射线）,计算出X0在该射线上的Y位置，如果Y>Y0则说明：该P0点在线段P1、P2的下方，交点数+1；反之则为下方。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public static bool checkPosInPolygon(List<Vector3> PosList, Vector3 checkPos)
{
    if (PosList == null || PosList.Count <= 0)
    {
        return false;
    }

    int num = 0;
    for (int i = 0; i < PosList.Count; i++)
    {
        Vector3 curPos = PosList[i] ;
        Vector3 nextPos = PosList[(i + 1) % PosList.Count] ;

        if (checkPos.y >= Mathf.Max(curPos.y, nextPos.y) || checkPos.y <= Mathf.Min(curPos.y, nextPos.y))
        {
            continue;
        }

        float lineSlope = (curPos.x - nextPos.x) / (curPos.y - nextPos.y);
        float linePosx = (checkPos.y - curPos.y) * lineSlope + curPos.x;
        if (linePosx < checkPos.x || Mathf.Approximately(linePosx, checkPos.x))
        {
            num++;
        }
    }
    return (num % 2 != 0);
}